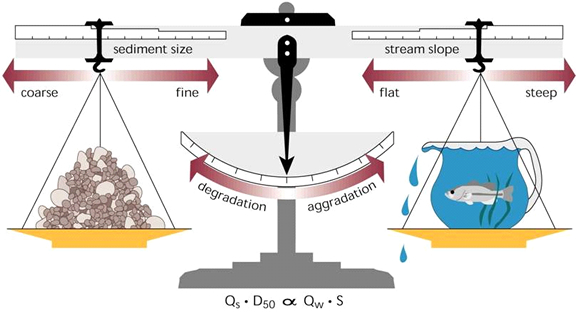
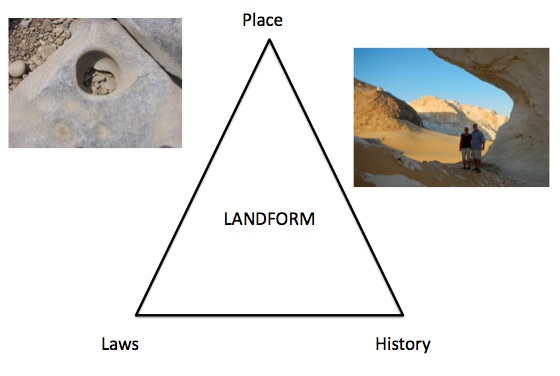
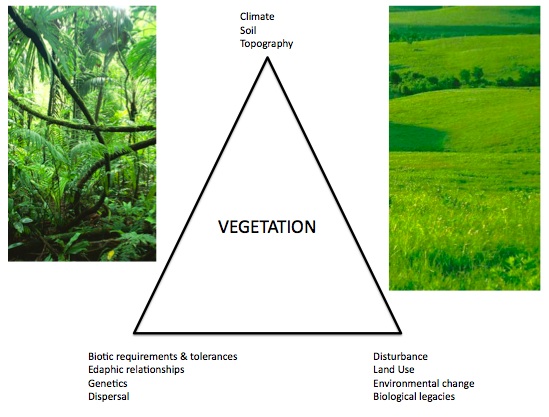
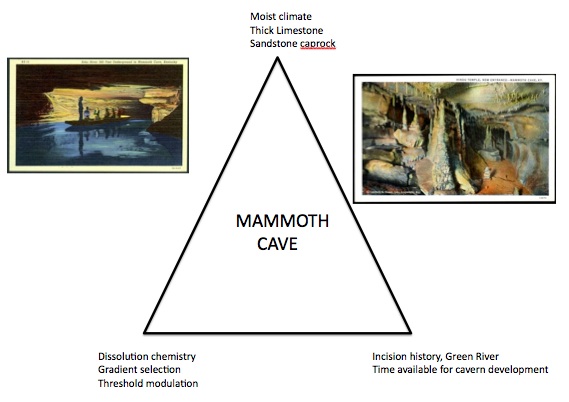
I get frustrated sometimes with the way university administrators are fixated on marketing and branding, and on “student success” implicitly defined as processing as many passing grades as possible (not just at UK; the phenomenon is a pandemic). Sometimes to relieve my frustrations I make things such as the flier below to amuse myself.

We’re supposed to advertise our courses to make them attractive to students, and to keep them entertained once they are in the class. If they don’t show up, it is the professor’s fault for not being entertaining enough.
I sent the flier to some colleagues in the department, none of whom recommend actually using it (I think I can safely assume that few, if any, potential GEO 130 students will read this blog). However, it has stimulated some interesting discussions.
One of my colleagues who teaches the same course generally has the same philosophy as me, with one exception—he takes attendance and has strict standards. Attendance and grades are better in his sections than in mine, and good on him for that. However, I have always thought that part of the university educational experience involves learning the values of reliability, time management, and taking responsibility for what you do (or don’t do). These students are, after all, legal adults. Thus, while the poor performers who didn’t have “successful outcomes” didn’t learn any physical geography and Earth system science to speak of, I like to think they learned a key lesson about the importance of showing up (all those who failed and the vast majority of those who withdrew or made D’s in my class in the last 3 years had zeros on one or more homeworks or exercises that they failed to turn in or show up for).
Others are adapting to the limited attention span of those for whom watching an entire music video represents a major time commitment. How can those folks be expected to sit through a 50 or 75-minute lecture or discussion? I genuinely applaud those who are so adapting and reaching some of these students on their own terms.
But shouldn’t our students also be trained, in at least some of their courses, to pay attention and concentrate on things that may not always be entertaining? Won’t they have to do that eventually in the examination or emergency room, in the courtroom or the boardroom, or on the other side of the classroom? Won’t they need to focus for extended periods of time at or in their research sites, job sites, construction sites, labs, battlefields, control towers, and cockpits? Won’t they have to sit through sales meetings, public hearings, briefings, press conferences, and the like?
Others have written much more eloquently on trends in higher education, including the commodification of college education and the pervasive student-as-customer model that’s been growing stronger at least since university administrators jumped on the George Deming bandwagon in the late 1980s and various other retail-education bandwagons since then. Those who think as I do have lost this war for the soul of the university long ago, but I’d sure like to think there is still a place for the vanquished old-school types in Higher Education, Inc.
Getting back to GEO 130, and the fact that this course, like physics, chemistry, math, and many other science/math classes, has higher rates of failure & withdrawal and lower grade point averages than non-STEM1 courses another of my colleagues had this to say:
“I am for a pluralistic approach, let there be multiple styles and content deliveries for 130 . . . that is a strength. Humans like human ideas, first and foremost, that's how we've become who we are as a culturally-mediated species. I think it will always be a hard sell to get most undergrad students to transcend their/our (necessary, complex, and fascinating) anthropocentrism to think only about Milankovitch cycles, global atmospheric circulation, and tidal bores (no pun intended). We have to keep these subjects on the table even if kinda unfun, lest the whole world go down the rabbit hole of all topics must be fun, familiar, and valuable insofar as they can be parsed down to a twittered opinion.”
Well said—I’m just tryin’ to stay out of the rabbit hole.
1For those who are, perhaps blessedly, not up on the latest edu-speak, STEM stands for Science, Technology, Engineering, and Mathematics.