By Richard LeComte
LEXINGTON, Ky. -- Pick an integer -- any integer -- between zero and 15. Then look through the special cards Richard Ehrenborg has up his sleeve. Not only can he use the cards to figure out what number you picked, but he can do it even if you lie once, through mathematical principles.
 Doesn’t add up? Oh, but it does. To explain the trick, Ehrenborg takes readers back to code corrections in transmitting data over communication networks. He uses his cards to explain key mathematical concepts to his students.
Doesn’t add up? Oh, but it does. To explain the trick, Ehrenborg takes readers back to code corrections in transmitting data over communication networks. He uses his cards to explain key mathematical concepts to his students.
“I teach math majors and computer science majors about this math, so I wanted to show them these applications,” Ehrenborg said. “All this information technology, number theory and abstract algebra actually have this very practical application.”
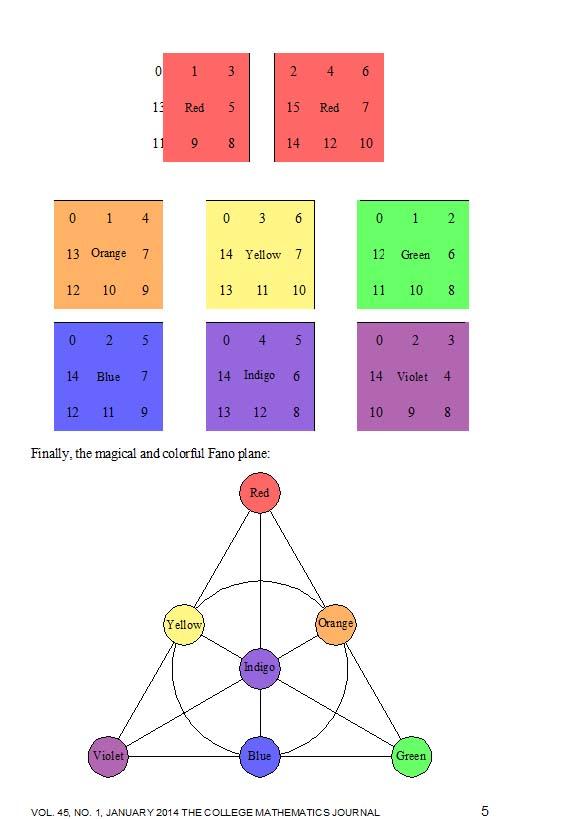
Ehrenborg recently published a paper titled “Fano, Galois, Hamming and a Card Trick.” He begins by showing how, in a popular card trick, a mathematician can print out four cards with eight numbers in certain sequences and ask a partner to pick an integer between 0 and 15. The partner then asks four “yes-no” questions about whether the number is on a card; the mathematician can guess the partner’s number by adding up the upper-left-hand numbers of the cards that drew a “yes.”
But what if your friend lies once? Then this first trick fails. The mathematician needs another, more involved trick. To perform this trick, the mathematician first needs more cards. This requires some heavy-duty math, including an error-correcting system called the “Hamming code,” which was originated by Richard Hamming, a pioneer in the mathematics of computers and telecommunications, who worked at Bell Labs in the 1940s.
“The first nontrivial Hamming code is a code of length 7 (bits) that has 16 code words and can correct one error," Ehrenborg said. “This means that if your friend thinks about an integer between 0 and 15, is willing to answer seven yes/no questions and lies at most once, you should be able to determine which number your friend is thinking about.”
The whole card trick illustrates how Hamming codes and abstract algebra can correct a transmission error in telecommunications. Math can take a signal sent in binary code and “fix” a blip in the transmission that might otherwise render the message unreadable. For example, in a CD player, the laser reading the disc will stumble upon an error created by a flaw on the disc, but through this code correction the player can figure out what the music really should be and correct it on the fly.
“You want to send four bits – and remember, four bits means two choices, then two choices, then two and finally two choices, so 16 possibilities,” he said. “So instead of this four-bit message, I’m going to send seven bits. If you lose the one bit that changed, then we can still reconstruct what the code was. We have 16 code words of length seven, and if one of them switches, we can still see which one is wrong and we can correct the error and determine the four original bits.”
For the trick, Ehrenborg uses what is known as the Galois field of eight elements. Using this field, he constructed a series of cards which he can use to narrow down the number the partner is thinking of and to create a system where, if he finds an inconsistency in his partner’s responses, he can fix it.
“There’s this abstract notion in math called a field," he said. “A field is basically a set of numbers that you can add, multiply, subtract and divide. There are fields that are finite – they are small – and they were discovered at the end of the 19th century. They are named after the French mathematician named Évariste Galois. Galois was killed in a duel at age 20. The legend has it that the night before the duel he wrote down all his mathematical ideas, and that is how people found out what a genius he was.”
To set up the trick, Ehrenborg color-coded the cards after the seven colors of the rainbow: red, orange, yellow, green, blue, indigo and violet. Each card has eight numbers on both sides. To help the magician to decode the Hamming code, Ehrenborg uses a mathematical figure known as the “Fano plane.” The Fano plane is a geometry consisting of seven points and seven lines. The seven points are also color coded after the rainbow. For each card he asks a question and according to the answer, “yes” or “no,” he places the card either up or down on the associated point on the plane.
“After placing out the seven cards on the Fano plane, look for the number 0,” he said. “Furthermore, when it appears, it is conveniently located in the upper left corner of each card. Looking at the zeros and using the geometry of the plane, you could see if your friend told the truth seven times or lied once. If the configuration of zeros is ``good’’, then your friend tells the truth every time. Look for the unique number that is on all the cards. It is the number your friend had in mind. If you see a ``bad’’ configuration, then you know that your friend lied one time.”
At that point, the mathematician-magician can look at the bad configuration, determine through quick calculation which card to turn over and what the secret number is. All of this through a rule designed to be easy such that it can be done in your head and allow the result to be magical.
Creating the cards was complex and required the use of several aspects of algebra and geometry, but the result is intended to be fun: A participant can “lie,” but with these rules, the magician-mathematician can “see” the error and quickly predict the number.
“My sincere hope is that any budding mathematicians can perform this trick," Ehrenborg said. “Remember that a magician never reveals his tricks, so do not tell your friends how useful finite fields are.”
